|
|

|
|
Quản lý, phân tích số liệu |
   |
|

|

|
| Trang chủ
>
Main menu
>
Phương pháp luận
>
Quản lý, phân tích số liệu | Kiểm tra mối tương quan giữa các biến bằng phương pháp vẽ biểu đồ và kiểm định sử dụng STATA | Trong phân tích số liệu và thống kê học, phân tích tương quan là một cách để đo lường mối liên quan giữa hai hay nhiều biến với nhau. Trong nghiên cứu khoa học chúng ta thường dựa vào mối liên quan giữa các biến để tính toán và dự báo sự thay đổi của một biến dựa vào thông tin mà chúng ta biết được về các biến liên quan đó. Ví dụ như dựa vào mối tương quan giữa thu nhập và giáo dục, chúng ta có thể thấy những người có trình độ học vấn cao hơn sẽ có thu nhập cao hơn. Khi chúng ta biết được trình độ học vấn của một người, ta có thể dự đoán được thu nhập trong tương lai của họ.
Trong bài này, thongke.info sẽ giới thiệu cụ thể mối tương quan giữa hai biến bằng các phương pháp vẽ đồ thị và sử dụng các hệ số tương quan sử dụng phần mềm Stata.
Vẽ đồ thị là phương pháp đầu tiên thường được sử dụng để xem xét mối tương quan giữa hai hay nhiều biến nhằm cung cấp cho ta một cái nhìn ban đầu về mối quan hệ giữa các biến này. Từ đó chúng ta sẽ có quyết định có cần thiết phân tích mối tương quan giữa các biến này không, có thể tiến hành các phân tích sâu hơn như phân tích hồi quy hay không?
Khi nhìn vào một biểu đồ mô tả mối tương quan chúng ta cần chú ý vào các điểm sau:
- Hình thái của mối tương quan tuyến tính, hình cung (curve)…
- Xu hướng của mối tương quan: thuận (positive) hay nghịch (negative)
- Khả năng dự đoán của mô hình (dựa vào đường fitedline)
- Các giá trị ngoài khoảng (outliers)
1. Mối tương quan giữa biến liên tục và biến liên tục
Trong thống kê mô tả, để biểu thị mối tương quan giữa biến liên tục và biến liên tục ta sẽ sử dụng biểu đồ chấm điểm rải rác (scatter)
*Lênh Stata: vẽ biểu đồ chấm rải rác (scatter)
twoway (scatter BMI m131a) (lfit BMI m131a)
twoway (scatter nr3 age) (lfit nr3 age)
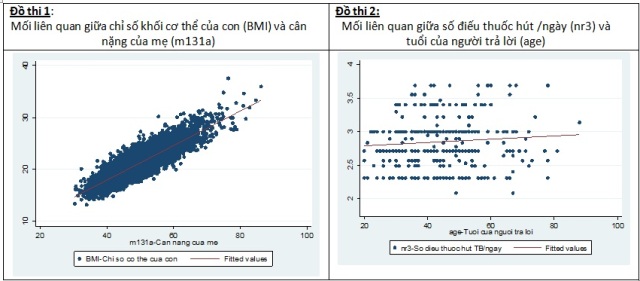
Theo đồ thị 1 ta có thể nhận thấy giữa hai biến chỉ số khối cơ thể của con (BMI) và cân nặng của bà mẹ (m131a) có mối quan hệ tuyến tính chặt chẽ với nhau và là mối tương quan thuận (positive). Dựa vào đường fited line ta thấy rằng chiều cao của mẹ dự đoán tương đối tốt sự thay đổi của chỉ số BMI của con. Ngoài ra ta cũng nhận thấy có xuất hiện một số giá trị ngoài khoảng của 2 biến này (các chấm rời rạc nằm cách xa đám mây).
Bằng phương pháp vẽ đồ thị, ta thấy giữa biến mối tương quan giữa chỉ số BMI của con và cân nặng của bà mẹ tương đối chặt chẽ với nhau. Tuy nhiên đó chỉ là đánh giá quan sát, để khẳng định độ mạnh yếu của mối tương quan này chúng ta cần sử dụng đến các kiểm định hệ số tương quan (r). [đã được thongke.info trình bày trong một bài riêng biệt trong mục Phương pháp luận/ “quản lý phân tích số liệu”]
Đối với các biến liên tục, trước khi kiểm định hệ số tương quan ta cần xác định biến đầu ra có phân phối chuẩn hay không để quyết định những kiểm định phù hợp (Xem thêm nội dung kiểm tra phân phối chuẩn của biến trong mục “quản lý phân tích số liệu”]).
- Kiểm định pearson được dùng để kiểm định hệ số tương quan giữa 2 biến liên tục có phân phối chuẩn
- Kiểm định spearman được dùng để kiểm định hệ số tương quan giữa 2 biến liên tục không có phân phối chuẩn
Phiên giải kết quả hệ số tương quan (r):
r<0.3: tương quan yếu
r=0.3-0.5: tương quan trung bình
r>0.7 tương quan rất chặt chẽ (r càng gần 1 tương quan càng mạnh)
Trong ví dụ của chúng ta giả định như sau:
- Biến chỉ số cơ thể của con (BMI) và cân nặng của bà mẹ là biến không có phân phối chuẩn.
- Biến số điếu thuốc hút TB/ngày và tuổi của người trả lời phỏng vấn (age) là biến có phân phối chuẩn.
Như vậy:
*Kiểm định spearman cho 2 biến liên tục không có phân phối chuẩn (BMI và m131a)
spearman BMI m131a
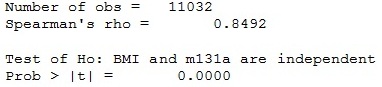
Theo kết quả phân tích này ta thấy rằng có mối tương quan chặt chẽ giữa biến BMI của con và cân nặng của bà mẹ (r=0.8)
* Kiểm định pearson đối với hai biến có phân phối chuẩn (nr3 và age)
pwcorr nr3 age, star(0.5)

Kết quả này cho thấy mối tương quan giữa số điếu thuốc hút TB/ngày hầu như không có mối liên quan với tuổi của người trả lời (r<0.1)
2. Tương quan của biến liên tục và biến phân loại
Để mô tả mối tương quan giữa biến phân loại và biến liên tục, ta sử dụng đồ thị boxplot.
Trong ví dụ này chúng ta muốn tìm hiểu mối liên quan giữa chỉ số cân nặng theo tuổi của trẻ (waz06) và nhóm chỉ số BMI của bà mẹ (BMI_new)
Lệnh stata:
graph box m135a, over ( BMI_new)
Đồ thị 3: Mối liên quan giữa biến cân nặng của trẻ (m135a) và nhóm BMI của bà mẹ (BMI_new)
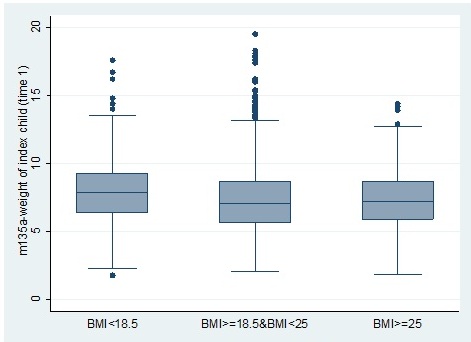
Boxplot (biểu đồ box-and-whisker) được sử dụng để so sánh một biến số (ví dụ cân nặng trẻ) ở các nhóm (chỉ số khối cơ thể của mẹ) khác nhau qua 5 giá trị: 1) giá trị thấp nhất (minimum), 2) 0-25% giá trị (lower quartile), 3) Trung vị (đường kẻ giữa box), 4) 75%-100% giá trị (upper quartile), và 4) giá trị cao nhất của biên (maximum). Boxplot cũng chỉ ra các giá trị bất thường - outliers.
Nhìn vào biểu đồ ta sự phân bố cân nặng của trẻ ở các nhóm BMI của bà mẹ tương đối là đồng đều, tuy nhiên thấy trung vị cân nặng của trẻ ở 3 nhóm BMI của bà mẹ có sự khác nhau. Cân nặng trung vị của trẻ có bà mẹ có BMI<18.5 dường như cao hơn so với 2 nhóm còn lại.
Để kiểm tra khẳng định sư khác nhau cũng như mối liên quan giữa nhóm BMI của bà mẹ và cân nặng của con. Chúng ta sử dụng lệnh phân tích, so sánh trung vị giữa nhiều nhóm. Ở đây biến cân nặng của con không có phân phối chuẩn nên chúng sẽ sử dụng kiểm định kruskal-wallis.
tabstat m135a, by(BMI_new) stats(n median)
(lệnh chạy so sánh trung vị cân nặng của con ở các nhóm BMI của mẹ)

kwallis m135a, by(BMI_new)
(lệnh kiểm định so sánh giá trị trung vị)
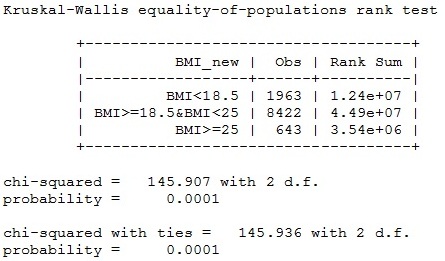
Kết quả kiểm định cho thấy sự khác nhau về trung vị cân nặng của trẻ có bà mẹ thuộc các nhóm BMI khác nhau (p<0.001). Trung vị cân nặng của trẻ có bà mẹ thuộc nhóm BMI<18.5 cao hơn so với các nhóm khác.
3. Tương quan giữa biến phân loại và biến phân loại
Bar graph được sử dụng để mô tả mối tương quan giữa hai biến phân loại với nhau
graph bar (sum) stunt,over(sex)
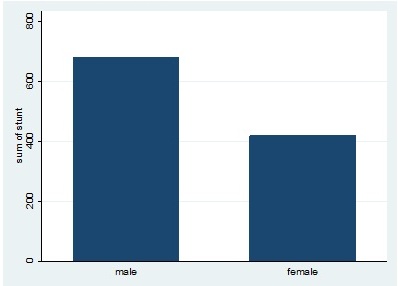
Theo biểu đồ, ta thấy số lượng trẻ nam bị thấp còi nhiều hơn số trẻ bị thấp còi là nữ. Ta có thể nghĩ đến có mối liên quan giữa tình trạng thấp còi của trẻ (stunt) và giới tính (sex). Để kiểm tra có mối tương quan này chúng ta sử dụng kiểm định khi bình phương (X2) với 2 biến phân loại
tab stunt sex, col chi2
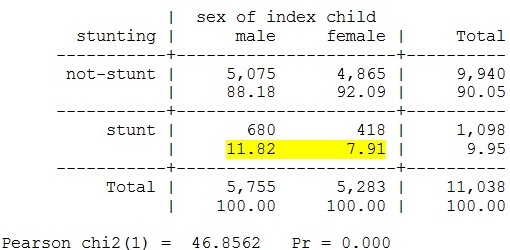
Kết quả kiểm định cho ta biết có mối liên quan giữa tình trạng thấp còi và giới tính của trẻ (p<0.001). Có 11,8% trẻ nam bị thấp còi trong tổng số trẻ nam trong khi đó tỉ lệ này ở trẻ nữ chỉ là 7,9%
Nguyễn Thị Trang
Nguyễn Trương Nam – thongke.info
Số lượt đọc:
41168
-
Cập nhật lần cuối:
23/08/2012 05:01:16 PM Hướng dẫn khôi phục dữ liệu sau khi gặp sự cố "corrupted"27/01/2013 11:11' PM Khi các bạn đang nhập liệu, nguồn của máy tính đột ngột bị mất (do lỏng đường dây, do mất điện đột ngột) mà bạn vẫn chưa kip lưu thì sau khi bạn khởi động lại máy tính và mở form epidata đang nhập liệu, máy tính sẽ báo lỗi như sau “One or more records are corrupted”.
Các bạn sẽ cố gắng tìm mọi cách để mở file đó ra, nhưng sẽ không thể mở được trực tiếp bằng phần mềm Epidata. Như vậy các bạn sẽ phải nhập lại toàn bộ số phiếu mình đã nhập trong form đó nếu bạn không có file backup.
Thongke.info xin giới thiệu với các bạn một cách rất đơn giản để khắc phục sự cố này. Thống kê và phương pháp phân tích số liệu - Sử dụng Stata12/01/2013 10:09' AM Xin chào các bạn, Xin chào các bạn,
- Khái niệm về thống kê cơ bản
- Lựa chọn trắc nghiệm thống kê
- Thực hành thống kê với Stata
Bảng thuật ngữ Dịch tễ học và Thống kê14/11/2012 11:49' AM Xin chào các bạn, Trong quá trình học tập và làm việc liên quan tới Dịch tễ học và Thống kê chắc hẳn các bạn đã từng được nghe hoặc biết đến các thuật ngữ như: Case-control Study, Cohort Study, Cross-sectional Study, Chi Square, Crude odds ratio, vv. Hay các thuật ngữ đươc viết tắt: OR, RR, EFp, EFe, vv. Hiện nay có nhiều thuật ngữ được dịch khác nhau dựa trên những quan điểm nhìn nhận khác nhau của các nhà Dịch tế và Thống kê học. Thongke.info xin giới thiệu bảng thuật ngữ Dịch tễ học và Thống kê trên quan điểm của thongke.info. Những vấn đề cơ bản của thống kê thực hành30/10/2012 09:58' AM Thống kê thực hành không nhằm mục đích vào giải quyết những vấn đề lý thuyết của thống kê và thống kê toán. Thống kê thực hành bao gồm các nội dung của quá trình nghiên cứu thống kê cụ thể. Các nội dung này được tiếp cận nhất quán trên tư tưởng của thống kê toán, đặc biệt là phương pháp mẫu ngẫu nhiên trong nghiên cứu thống kê cũng như các công cụ cần thiết trong thực hành, nghiên cứu thống kê. Với mục đích nói trên, thống kê thực hành đề cập đến những nội dung cụ thể sau: Thống kê thực hành không nhằm mục đích vào giải quyết những vấn đề lý thuyết của thống kê và thống kê toán. Thống kê thực hành bao gồm các nội dung của quá trình nghiên cứu thống kê cụ thể. Các nội dung này được tiếp cận nhất quán trên tư tưởng của thống kê toán, đặc biệt là phương pháp mẫu ngẫu nhiên trong nghiên cứu thống kê cũng như các công cụ cần thiết trong thực hành, nghiên cứu thống kê. Với mục đích nói trên, thống kê thực hành đề cập đến những nội dung cụ thể sau: Thống kê mô tả26/10/2012 09:46' PM Thống kê mô tả luôn là cách thức mở đầu cho các phân tích thống kê nói chung và phân tích kinh tế xã hội nói riêng. Có nhiều cách hiểu và đánh giá vai trò của thống kê mô tả, với quan niệm thống kê mô tả là bước khai phá số liệu, các nội dung trong chương này trình bày thống kê mô tả với hai mục đích chính: một là, thống kê mô tả như một cách thức tổng hợp số liệu và mô tả các đặc trưng quan trọng của các biến; hai là, dùng thống kê mô tả phát hiện các đặc trưng và quan hệ tiềm ẩn trong tổng thể, đặc biệt là các quan hệ nhiều biến. Thống kê mô tả luôn là cách thức mở đầu cho các phân tích thống kê nói chung và phân tích kinh tế xã hội nói riêng. Có nhiều cách hiểu và đánh giá vai trò của thống kê mô tả, với quan niệm thống kê mô tả là bước khai phá số liệu, các nội dung trong chương này trình bày thống kê mô tả với hai mục đích chính: một là, thống kê mô tả như một cách thức tổng hợp số liệu và mô tả các đặc trưng quan trọng của các biến; hai là, dùng thống kê mô tả phát hiện các đặc trưng và quan hệ tiềm ẩn trong tổng thể, đặc biệt là các quan hệ nhiều biến.
Thongke.info xin giới thiệu với các bạn bài viết: thống kê mô tả, các bạn có thể download bài viết tại đây.
Thongke.info xin cám ơn PGS.TS Ngô Văn Thứ đã chia sẻ bài viết.
Phương pháp kiểm định tương tác trong phân tích số liệu nghiên cứu khoa học - Assessment of Interaction02/08/2012 09:36' AM Giới
thiệu
Đôi
khi, mối liên quan giữa hai biến bị thay đổi bởi một biến Bài đã đăng: Hướng dẫn sử dụng lệnh relate trong Epidata để kết nối các file dữ liệu có cùng một mã ID11/07/2012 05:35' PM Hướng dẫn
sử dụng lệnh relate trong Epidata để kết nối các file dữ liệu có cùng
một mã ID (ứng dụng trong điều tra nhân khẩu hộ gia đình).
Phần trước thongke.info đã giới thiệu tới các
bạn cách tạo form nhập liệu, cách viết lệnh consistency check trong Epidata. Phần
này thongke.info xin được giới thiệu tới các bạn lệnh relate trong Epidata.
Chúng ta sử dụng lệnh relate khi các bạn có
các rec file riêng biệt và muốn link các rec file đó lại với nhau với cùng một
mã ID.
Ví dụ: Khi
các bạn có một điều tra nhân khẩu hộ gia đình với mục tiêu là điều tra thông
tin chung của hộ gia đình, thông tin về từng thành viên trong gia đình. Phương pháp xử lý giá trị missing trong Stata05/07/2012 03:45' PM Trong quá trình thu thập số liệu, nhập liệu có những biến sẽ có giá trị missing. Nguyên nhân có thể do phỏng vấn viên quên hỏi, do nhập liệu viên nhập sót hoặc do thiết kế bộ câu hỏi có những câu hỏi chỉ dành riêng cho nhóm đối tượng nào đó. Ví dụ như hỏi về việc chăm sóc thai nghén sẽ chỉ hỏi ở những người phụ nữ đã từng mang thai, hay hỏi về sử dụng dịch vụ y tế trong 1 tháng qua thì sẽ chỉ hỏi với những đối tượng đã đến cơ sở y tế 1 tháng qua… Chúng ta cần phát hiện và xử lý các giá trị missing này để đảm bảo tính chính xác của các kết quả phân tích. a. Phát hiện các giá trị missing Quản lý số liệu17/06/2012 10:46' AM Thongke.info xin giới thiệu với các bạn bài viết về quản lý số liệu, trong bài viết sẽ cung cấp nhưng phương pháp: thiết kế bộ câu hỏi thu thập số liệu, thử nghiệm bộ câu hỏi trước khi nhập liệu, tạo bộ câu hỏi (.Ques, .Rec, .Chk), nhập số liệu (nhập hai lần), kiểm tra số liệu, kiểm tra logic và tính nhất quán của bộ số liệu, làm sạch số liệu (frequency, cross-tabs, bảng phân bố), và lưu trữ.
Các bạn có thể download bài giảng quản lý số liệu tại đây. Ứng dụng phân tích hồi quy (Regression)20/05/2012 01:22' PM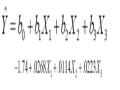 Trong quá trình học tập, nghiên cứu, và làm việc trong lĩnh vực nghiên cứu khoa học các bạn đã từng nghe đến phân tích hồi quy. Vậy hồi quy là gì? Và tại sao chúng ta cần phân tích hồi quy? Bài giảng ứng dụng phân tích hồi quy sẽ trả lời cho các bạn câu hỏi đó và đồng thời giới thiệu với các bạn các bước xây dựng mô hình hồi quy, hồi quy tuyến tính đa biến và hồi quy logic.
Tạo bảng trống/bảng giả cho phân tích số liệu (Dummy tables)20/05/2012 12:12' PM Xin chào các bạn,
Dummy tables là các bảng giả (mock tables) tạo ra trước khi phân tích số liệu, được tạo dựa trên câu hỏi nghiên cứu và kế hoạch phân tích, và giúp định hướng cụ thể các phân tích để trả lời câu hỏi nghiên cứu. Bảng dummy chính là kế hoạch phân tích chi tiết và cũng là công cụ để giúp thảo luận và thống nhất phân tích trong nhóm các nghiên cứu viên, vv. Nội dung bài viết: - Lý do tạo bảng trống - Dummy tables
- Các loại bảng trống
- Tạo bảng trống
- Giới thiệu các loại bảng trống
- Ví dụ tạo các loại bảng trống
Làm sạch số liệu và tạo biến trong SPSS20/05/2012 10:54' AM Làm sạch số liệu là một bước quan trọng để sử dụng số liệu trước khi phân tích. Làm sạch số liệu ban đầu có thể thực hiện ngay trong quá trình thực địa, nghĩa là khâu quản lý và giám sát chất lượng tại thực địa tốt. Điều này sẽ làm hạn chế các lỗi, sai sót trong bộ số liệu và việc sử dụng các phần mềm (SPSS, Stata) để làm sạch số liệu sau này sẽ tiết kiệm thời gian và đỡ phức tạp hơn. Các bạn có thể thao khảo bài viết "Giám sát chất lượng". Trong bài viết này, thongke.info sẽ giới thiệu với các bạn: - Cách làm sạch số liệu sử dụng phần mềm SPSS
- Tạo biến mới sử dụng phần mềm SPSS
- Kiểm tra phân bố chuẩn sử dụng phần mềm SPSS
Phân tích nhân tố khám phá (Factor analysis)18/05/2012 10:27' PM Thongke.info xin giới thiệu với các bạn bài trình bày về phân tích nhân tố khám phá (factor analysis). Bài viết sẽ trình bày 5 phần chính: Giới thiệu factor analysis, các bước trong factor analysis, thao tác thực hiện, đọc kết quả, và các phân tích khác sau khi thực hiện factor analysis.
| |
|

|
|
|
|
|
|
|

